Microphones: Levels & History

Before going further, you might want to re-visit the previous four installments of this series to refresh your memory of Sensitivity, Noise, SPL and Distortion. In the Sensitivity installment we introduced the concept of a ‘Goldilocks Zone’ around the preamp’s gain control – an ideal zone to keep the gain control within. In the Noise installments we looked at the sources of noise within the microphone and within the preamplifier (Brownian Noise and Thermal Noise) and what we can do to minimise noise in the captured and preamplified signal. In the SPL & Distortion installment we looked at clipping distortion and the related microphone specifications of Maximum SPL and Dynamic Range. All of the specifications discussed so far relate to the signal’s level.

Now it’s time to put them all together and see how they can help us choose a microphone that delivers a signal that remains within the preamplifier’s Goldilocks Zone, resulting in less noise and (hopefully) no audible distortion. But first we have to understand some basic concepts about signals. There’s a lot to get through here; if you’re impatient, incurious or still believe you can be an audio engineer by remembering settings shown on Youtube, you might want to skip to the next installment and review this one later for rationale and historical perspective.

ANALOGUE SIGNAL FUNDAMENTALS

To make sense of the microphone and preamplifier specifications related to signal levels, we need to understand some general principles of analogue signal levels, and the best way to do that is to begin with their limitations.

As we’ve learnt in the previous installments, everything that sound passes through has limits that determine how high and how low the signal level can go.

Noise

The lowest level the signal can go is determined by noise – whether it’s acoustic noise in the space the sound is passing through, Brownian noise in microphone diaphragms, thermal noise in analogue audio electronics, or quantisation noise in digital systems. The level of noise ultimately determines the lowest sound level that can be heard and/or the lowest signal level that can be captured; as the sound or signal level falls too far towards the noise, it becomes unintelligible and eventually inaudible.

Paradoxically, in digital audio systems we add noise to allow the signal to remain intelligible and audible at low levels. That noise is called dither and the process of adding it is called called dithering. Applying dither to a digital signal turns the grittiness of quantisation noise into a far more acceptable hiss – it’s usually louder than the quantisation noise, but it’s much less obtrusive. It’s also used in digital imaging to improve the visual perception of low resolution images, but dither is a topic for another time.

Distortion

The highest level the signal can go is determined by the point where the sound or signal’s waveform is altered due to a form of distortion known as ‘clipping’, where the peaks of the waveform are flattened as if they’ve been clipped off with scissors – as discussed in the previous installment. Clipping occurs in analogue audio circuits (including the circuits found inside condenser microphones and active microphones) when the signal’s Peak voltage level tries to exceed the maximum voltage used to power the circuit. It occurs in digital systems when the signal’s Peak digital value tries to exceed 0dBFS, which is the largest number the digital system can represent. Clipping also occurs in the air when the sound exceeds 194dB SPL, at which point the negative half-cycle of the waveform rarefies the air molecules to a complete vacuum – which is the highest possible negative atmospheric pressure. [This form of clipping is a problem for those who record fireworks, rocket launches, explosions and thunder storms because the sound is clipped by the air before it reaches the microphone, and no amount of gain tweaking, pad switching or mic swapping is going to change that. Interestingly, because it’s only clipped on the negative half cycles it is an asymmetric form of clipping, which introduces a different balance of harmonic distortion components compared to symmetrical clipping and can sometimes sound less obtrusive and, in some cases, more musical – as heard in electric guitar amplifiers.] In all cases, if the signal level goes too far into clipping we have a problem.

Because our focus in this installment is on signal levels, we’re going look at how the limitations of clipping and noise manifest in audio circuits such as microphone preamplifiers and digital audio systems, and how that influences our microphone choices. But first, a quick look at the three types of signal levels we encounter regularly in audio engineering: Mic Level, Line Level and Instrument Level.

Mic Level

Unless we’re using a microphone with a digital output (e.g. AES42, USB or MEMS), the signal presented at the output of our microphone is a very small analogue voltage that is typically measured in hundredths or thousandths of a volt. When converted to decibels it’s usually somewhere between -60dBu (0.000775V_RMS) and -20dBu (0.0775V_RMS). It’s referred to as Mic Level, and must be passed through a microphone preamplifier to bring it up to a useful level for processing and/or recording (i.e. Line Level).

Mic Level signals use balanced lines and XLR connectors. The patchbays in some professional recording studios allow cross-patching of microphone lines to preamplifier inputs via balanced Bantam TT patch leads and sockets, although mic patching is best done with XLR plugs and sockets. Most manufacturers of XLR connectors make the contact for pin 1 slightly longer than for pins 2 and 3 on their female XLRs (usually used as inputs) to ensure that pin 1 (ground) connects first, a useful safety feature. Microphone manufacturer Røde intentionally makes pin 1 slightly longer on their microphone output XLRs (which are male XLRs) for the same reason – a very good idea that unfortunately leads the uninformed to think there’s a manufacturing defect because one pin is longer than the others.

[To avoid thumps that could damage monitor speakers, headphones and ears, it is always good practice to mute the monitoring whenever you’re patching microphones – especially if you’re using phantom power, and even moreso if you’re patching with Bantam TT connectors (rather than XLRs) because their ring/tip/sleeve configuration means for a brief moment you could be providing the mic input with a huge input signal of +48V DC. That’s enough to damage passive monitor speakers, headphones, human hearing, and whatever credibility you might have established with the client.]

Line Level

The microphone preamplifier’s job is to amplify the Mic Level signal up to a useful level for further processing, which is usually referred to as Line Level.

Most Line Level signals use balanced lines with either XLR connectors, TRS jacks or the Bantam TT connections seen on the patchbays in professional recording studios. We’ll be talking more about Line Level signals shortly because the ultimate goal of the preamplifier is to get the Mic Level signal up to Line Level…

Instrument Level

Electric guitars, keyboards and other electronic musical instruments designed for live performance provide their outputs on 6.35mm TS sockets (one for mono, two for stereo), intended to be connected to an instrument amplifier. The signals they provide are often referred to as Instrument Level; they’re higher than Mic Level but lower than Line Level, typically sitting somewhere around -20dBu (0.0775V_RMS). They’re too low for most Line Level inputs but too high for most Mic Level inputs, and they’re usually unbalanced which means they’re okay for sending down short cables between the instrument and its amplifier, but not for sending down long cables between the stage and the mixing console in a sound reinforcement application. They’re usually connected to a mixing console or microphone preamplifier via a DI box, which drops the relatively high but unbalanced Instrument Level signal down to a relatively low Mic Level signal with a balanced output suitable for sending down longer cable distances and into a microphone preamplifier.

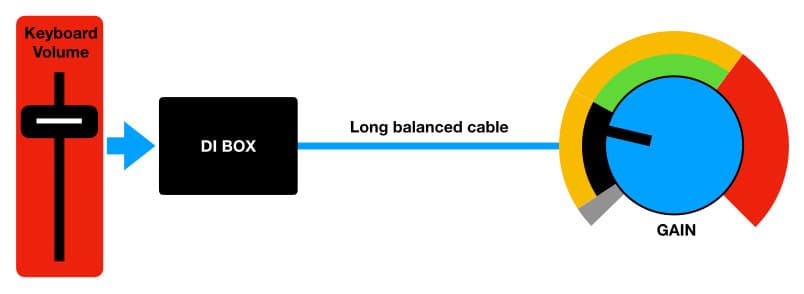
Some keyboards and rack-mounting modules provide a balanced Line Level output on either an XLR or TRS socket, and this should be used whenever possible to connect to a Line Level input.

When working with Instrument Level signals in situations where the instrument is close to the preamplifier or mixing console, finding the lowest noise connection while avoiding clipping is often a juggling game between the instrument’s output level and the preamplifier’s gain. Although the use of a DI box into a Mic Level input is common, in some cases a better signal quality can be achieved by plugging the instrument’s output directly into a Line Level input that has an adjustable Trim or Gain control.

Some interfaces, especially those designed for recording musicians, have an Instrument Level input with a 6.35mm TS socket that’s specifically designed for accepting Instrument Level signals. It should be the first choice for this application.

In all cases, finding the right balance between the instrument’s output level and the gain of the preamplifier, Instrument or Line input is important to minimise noise and prevent clipping – either from pushing the instrument’s output circuit into distortion, or from overloading the input of the DI box, Mic input, Instrument input or Line input. A good starting point is to have the instrument’s output level set to about 70% of maximum, although the actual signal level will be dependent on the patch, sample or clip in use.

[On the topic of patches, samples and clips used in live performance, it’s always worth tweaking the output level of each one so it has a similar perceived level as the others. This can be done by ear or with an SPL meter placed in front of the instrument’s amplifier, with the desired level stored in the user-memory as part of each patch, sample or clip. This makes the performer’s life easier on stage by minimising the need to reach out and adjust the volume after every change while trying to play their part. That, in turn, makes the live sound engineer’s job easier, and both improvements ultimately result in a better sounding gig.]

WHAT IS A SIGNAL?

Entire books have been written about audio signals and the many ways we can define and measure them.

The sine wave is the simplest signal of all (apart from absolute silence) and yet there are at least four ways of defining its level, or, more correctly, its amplitude. The illustration below shows one cycle of a sine wave (green) with a maximum positive amplitude of +1 and a maximum negative amplitude of -1. It also shows four different ways of measuring and defining the sine wave’s amplitude, as explained below.

Peak-To-Peak

We’ll start at the illustration’s far right with Peak-To-Peak, which is measured from the peak of the positive half-cycle to the peak of the negative half-cycle. In this example it has a value of two (from +1 to -1), but it’s worth noting that at no point on the signal’s waveform does it ever reach a value of two. In fact, in this example – which uses a symmetrical waveform where the positive and negative half-cycles are mirror images – the highest amplitude it ever reaches is half of the Peak-To-Peak value.

Peak-To-Peak measurements are usually indicated with the suffix ‘PP’, e.g. ‘_PP’. If the Peak-To-Peak amplitude of the sine wave in the illustration was measured in Volts (abbreviated to ‘V’), we would write its value as 2V_PP.

Peak-To-Peak measurements are mostly used when determining what is often called the swing of a signal; in other words, the difference between the maximum positive amplitude and maximum negative amplitude. The sine wave in the illustration has a swing of two volts. Peak-To-Peak measurements are useful when designing loudspeakers and power supplies for audio circuits, but they’re not useful for our purposes here.

Peak

As seen in the illustration, the Peak value is measured from zero to the signal’s maximum positive or negative peak. In the illustration it has been measured to the maximum positive peak and has a value of +1. Because the sine wave is a symmetrical waveform it’s safe to assume the negative peak will be the same value as the positive peak (unless it has a DC offset), but with inverted polarity. Unlike the Peak-To-Peak value, we can see that the signal’s waveform does actually reach the Peak level – albeit momentarily.

Peak measurements are usually indicated with the suffix ‘P’, e.g. ‘_P’. If the Peak amplitude of the sine wave in the illustration was measured in Volts (V), we would write its value as 1V_P.

Peak measurements are useful for determining how close a signal is to a device’s Maximum Level, which is the highest signal level possible before distortion occurs due to clipping. It’s commonly used in the meters found on digital audio equipment, where 0dB is the Maximum Level before clipping. Peak metering systems consider the Peak values of both the sides of the waveform (i.e. the positive and negative half cycles) to make sure nothing sneaks past due to a non-symmetrical waveform or a DC offset.

Average & RMS

The problem with Peak measurements is that many audio signals (including the sine wave in the illustration) are only at their Peak level for a brief portion of their duration. A Peak measurement provides a good indication of the highest amplitude the signal goes to, which is useful for preventing distortion due to clipping, but it doesn’t tell us much else about the signal – for example, how loud it will be compared to other signals with the same Peak value, which we will call its relative perceived loudness. For values that allow us to compare the relative perceived loudness of different signals, Average and RMS measurements are more useful than Peak measurements.

The Average value for a sine wave is calculated as follows:

Average = 0.637 x Peak

Average measurements are usually indicated with the suffix ‘AV’, e.g. ‘_AV’. The sine wave in the illustration has a Peak amplitude of 1V, therefore its Average amplitude is:

0.637 x 1 = 0.637V_AV

RMS is an acronym for ‘Root Mean Square’, which describes the mathematical process of determining its value. Electrical engineers used to refer to it as the ‘heating value’, which hints at its origins. The RMS value for a sine wave is calculated as follows:

RMS = 0.7071 x Peak

RMS measurements are usually indicated with the suffix ‘RMS’, e.g. ‘_RMS’. The sine wave in the illustration has a Peak amplitude of 1V, therefore its RMS amplitude is:

0.7071 x Peak = 0.7071V_RMS

Measurements given in dBu, as shown earlier in this installment, are based on RMS values where 0dBu = 0.775V_RMS. A value of -20dBu means the signal is 20dB lower than 0dBu, which means it is 20dB lower than 0.775V_RMS, which is 0.0775V_RMS. As a quick dB hack, it’s worth knowing that 20dB represents a factor of 10, so -20dB means ÷10, and +20dB means x10. Hence, -20dBu is 1/10th of 0dBu which is 1/10th of 0.775V_RMS.

Note that the formulas for Average and RMS given above only apply to sine waves. The formulas for calculating the Average and RMS values of other waveforms increases in complexity with the waveform’s complexity.

For audio applications the Average and RMS values both provide a better indication of a signal’s relative perceived loudness. However, neither is as good as the LUFS metering system when it comes to comparing and matching the relative perceived loudness of different signals. You’ve probably heard a lot about LUFS (Loudness Units Full Scale) in reference to mastering mixes for uploading to streaming services. Perceived loudness is usually a mastering topic, so what does it have to do with choosing microphones and setting gain? Keep on reading…

MICS, GAIN & LOUDNESS?

All digital audio devices have Peak metering to help us prevent signal levels from exceeding the Maximum Level (0dBFS) and distorting. Some DAWs also offer RMS and/or Average metering that is typically superimposed over the Peak level, and there are plug-ins and apps that offer many different metering options.

We cannot use Peak levels to compare the perceived loudness of different audio signals because the human ear/brain system does not pay much attention to short-term peaks like those found in a percussive sound – instead, it judges a sound’s loudness using a complex averaging system that requires considerable signal processing capabilities to emulate.

The illustration above shows the waveform of a vocal track (blue), with the waveform of a series of kick drum hits (red) superimposed over it. Both tracks have been adjusted to reach the same Peak value, but they don’t have the same perceived loudness. The vocal track is considerably louder than the kick drum track because much of the kick drum’s energy exists as a short-term peak or ‘transient’ that doesn’t have much impact on the perception of loudness, and the rest of its energy is in the low frequency spectrum where human hearing is less sensitive than it is to frequencies in the vocal range.

In the illustration below, the level of the vocal track has been reduced so it has the same perceived loudness as the kick drum track. The kick’s Peak level is considerably higher than the vocal’s Peak level, and yet its perceived loudness is the same.

Crest Factor

In audio terms, a signal’s Crest Factor describes the difference between a signal’s Peak level and its Average level, and is usually given in decibels. Percussive sounds (such as the kick drum in the examples above) have a high Peak level but a low Average level, giving them a high Crest Factor but low perceived loudness. In comparison, non-percussive sounds (such as the vocal in the examples above), have a much lower Crest Factor which, in turn, allows a higher Average level and therefore a higher perceived loudness

A signal with a high Crest Factor will need more Headroom (see below) than a signal with the same Average level but a lower Crest Factor.

When mastering audio to conform to the limited dynamic range requirements of streaming services, one of the goals is to reduce the signal’s Crest Factor so that the Peak level is lower. This allows the Average level to be raised higher – thereby increasing the perceived loudness.

What’s this got to do with choosing microphones and setting gain? Keep on reading…

VU & LUFS

The problem of indicating perceived loudness brought us the VU meter (late 1930s) as a way of maintaining consistent loudness in broadcast applications where the program material was regularly switching between different announcers’ voices and different music selections. ‘VU’ stands for Volume Unit, where ‘volume’ refers to perceived loudness rather than cubic space. The VU meter uses relatively slow ballistics (i.e. how fast the needle can move) with attack and release times of around 300ms (0.3s) that ultimately give it an averaging effect. The needle moves too slowly to keep up with the transient peaks of the kick drum shown earlier, conveniently preventing them from causing misleading perceived loudness levels. The basic idea is (or was) that if all signals going to air have approximately the same level on the VU meter then they should have approximately the same perceived loudness, so there should be no sudden surprises when switching between announcers’ voices and/or the music that was popular at the time. The VU meter worked well enough for this application, but its shortcomings became obvious with the introduction of multitrack recording and the associated close-miking of individual musical instruments – particularly when working with percussive/plucked sounds with fast transients and short decays, such as the kick drum shown earlier.

Contemporary digital streaming systems are faced with the same problem as the early analogue broadcasters except they need to switch between many different types of sound sources (narration/dialogue, different genres of music and sounds, movies, etc.) on demand, and, unlike the early broadcasters, there is no engineer monitoring what’s ‘going to air’ in real-time to make adjustments when things get too loud or too soft. This has lead to the refinement of the LUFS metering system, as described in the EBU R128 standard and based on recommendations in ITU BS1770. It’s a far more accurate indicator of perceived loudness than the VU meter; if two signals have the same integrated (i.e. averaged over the duration of the signal) LUFS value they will probably have the same perceived loudness overall. Individual streaming services have settled on specific integrated LUFS levels to keep their playback loudness consistent – which is why you can usually swipe between numerous videos on Youtube or numerous pieces of music on Spotify without experiencing any significant changes in perceived loudness. Integrated LUFS metering can provide very accurate indications of perceived loudness, but what’s that got to do with choosing microphones and setting gain? Keep on reading…

NOMINAL OPERATING LEVEL

VU meters are still popular on analogue audio devices, and all analogue audio devices share the limitations of noise and distortion mentioned earlier. Noise is a problem when the signal’s level gets too low, and distortion is a problem when the signal’s level gets too high. Because audio signals can vary greatly between their Peak levels and their perceived levels (whether measured as Average, RMS or LUFS), professional analogue audio equipment follows a concept known as a Nominal Operating Level (NOL) – a recommended signal level that’s high enough to keep the perceived level above the noise but (hopefully) low enough to prevent the Peak level from distorting due to clipping. The NOL is represented as 0dB on a VU meter and is, therefore, referred to as ‘0dBVU’. Signals that are at the NOL are also referred to as ‘Line Level’, as discussed earlier.

In professional analogue audio equipment the NOL of 0dBVU is standardised to a signal level of +4dBu, which is equivalent to a voltage of 1.228V_RMS when measured using a 1kHz sine wave as the signal. In other words, if a 1kHz sine wave was passed through the equipment and its level was adjusted to read 0dBVU on the VU meter, it will have a voltage of 1.228V_RMS. This standard allows the numerous items in the analogue recording studio to be calibrated to the same NOL of +4dBu so that 0dBVU out of the mixing console results in 0dBVU into the tape recorders and effects processors, and vice versa. With everything calibrated to the same NOL, all the individual devices in the analogue audio system essentially become one big integrated device. If we get the level right at the preamplifier it should be right throughout the rest of the system – at least until we start pushing faders away from their 0dB (or Unity) positions, applying EQ, using compression, and doing other things that affect a signal’s level.

If we know an analogue audio device’s NOL, along with its Maximum Level (the level where clipping distortion occurs) and its Noise Floor (the level of its noise), we can calculate its specifications for Dynamic Range, S/N Ratio and Headroom, as shown below.

We’ve seen how these specifications relate to microphones in earlier installments of this series. Let’s see how they relate to other analogue audio equipment in the signal path, and how they’re specified.

S/N Ratio

In earlier installments we saw that the microphone specification for S/N Ratio is defined as the difference between 94dB SPL and the microphone’s Equivalent Noise Level or Self Noise. An SPL of 94dB at the diaphragm was used as a reference point to represent the signal. In professional analogue audio equipment the reference point is the device’s NOL, and the S/N Ratio is defined as the difference between the NOL and the device’s Noise Floor. It’s specified in dB, and a bigger value means a higher S/N Ratio – which means lower noise. As shown in the previous illustration:

S/N Ratio = Nominal Operating Level – Noise Floor

Headroom

The Headroom specification describes the difference between a device’s NOL and its Maximum Level. In other words, how far the signal can go above the NOL before it reaches clipping. As shown in the previous illustration:

Headroom = Maximum Level – Nominal Operating Level

Most professional analogue audio devices offer at least 20dB of Headroom, and anything less is usually considered insufficient. That’s a useful piece of information we’ll come back to shortly when we look at how digital devices fit into the analogue world of sound itself. For any given NOL, more Headroom is generally considered better than less. The Peak meters seen on digital audio devices are sometimes referred to as ‘Headroom meters’ because they show how much Headroom is left between the signal’s Peak and the device’s Maximum Level.

Headroom is rarely, if ever, quoted for microphones but it can be calculated as the microphone’s Maximum SPL specification minus 94dB SPL. In essence, we can use 94dB SPL as the microphone’s Nominal Operating Level just as we do when calculating the microphone’s S/N Ratio.

Dynamic Range

In the previous installment we saw that the microphone’s Dynamic Range specification described the difference between the level of its noise and its Maximum SPL specification (the point where clipping occurs). The same logic applies to the Dynamic Range of professional analogue audio equipment – it’s defined as the difference between the device’s Noise Floor and its Maximum Level. It’s specified in dB, and a bigger value ultimately means the device has a larger or ‘wider’ Dynamic Range; this means it could have a better S/N Ratio, more Headroom, or both. As shown in the previous illustration:

Dynamic Range = Maximum Level – Noise Floor

And, also as shown in the illustration:

Dynamic Range = Headroom + S/N Ratio

ALIGNMENT LEVEL

Things are different in the digital world. The digital system’s inherent noise is so low compared to an analogue system’s noise (especially when using analogue tape recorders) that the need for a NOL is not immediately obvious. The main requirement is to ensure the signal’s Peak level doesn’t exceed the digital system’s Maximum Level, which is represented as 0dBFS on the digital system’s metering. The ‘FS’ in ‘dBFS’ stands for ‘Full Scale’, where 0dBFS represent the Maximum Level (or clipping level) and exceeding it results in distortion. With the exception of 0dBFS, all other dBFS levels are given in negative numbers and represent how far the signal’s Peak level is below the Maximum Level; for example, a level of -12dBFS means the signal’s Peak level is 12dB below the level where clipping occurs. It seems simple enough, but there’s more to it than that…

At some point we need to get an analogue signal in to the digital system from our microphones and other analogue sound sources, and at some point we need to get an analogue signal out of the digital system to connect to headphones, monitors or external analogue processors. This means the digital system must ultimately have analogue input and/or output circuits (i.e. analogue-to-digital converters and digital-to-analogue converters), and for the analogue parts of those circuits all of the analogue specifications shown above are still applicable. Furthermore, if our professional digital equipment is going to be integrated with our professional analogue equipment (e.g. using a DAW with an analogue mixing console or processor, or running plug-ins that model/emulate vintage analogue processors), it needs to have a digital equivalent to the professional analogue equipment’s NOL – a reference level that conforms to +4dBu while allowing sufficient headroom for the signal from the analogue devices. This is usually referred to as an Alignment Level, and is the digital system’s equivalent to the analogue system’s NOL.

What’s that got to do with choosing microphones and setting gain? Keep on reading…

0dBFS ≠ 0dBVU

Most of the early digital multitrack tape recorders (e.g. Sony 3348, Mitsubishi X850) that were designed for use in analogue multitrack studios had Alignment Levels between -19dBFS and -24dBFS for +4dBu, maintaining the analogue studio’s NOL and allowing them to be installed directly in place of an analogue multitrack recorder. As an added benefit they offered more Headroom than the analogue tape recorders they replaced, which rarely offered more than 12dB above the NOL (0dBVU) before entering tape saturation – the magnetic equivalent to clipping that can be euphonic in small doses.

One interesting problem with the early digital multitrack tape recorders was that, although their inputs and outputs conformed to the analogue studio concept of +4dBu NOL, their metering used the dBFS scale where 0dBFS represents the Maximum Level – which is not the same as the NOL represented by 0dBVU.

This caused confusion among experienced sound engineers who had honed their craft in a world where signal levels were supposed to be kept around 0dB on a metering system designed to show a form of relative perceived loudness (the VU meter), and where there had always been Headroom to go above 0dB. How do they transfer their level setting skills to a digital metering system where 0dB is the Maximum Level, rather than the NOL, and cannot be surpassed?

A faithful adherence to the old analogue rule of keeping signal levels as close to 0dB as possible, combined with the new digital rule of not allowing the signal to go above 0dB, highlighted the misunderstandings between 0dBVU and 0dBFS. In many early hybrid studios (analogue consoles with digital multitrack tape recorders) the mixing console’s bus outputs were often pushed 12dB or more above the console’s NOL of 0dBVU to get signal levels as close as possible to 0dBFS on the digital tape recorder’s meters, as engineers did what they believed they were supposed to do by keeping levels close to 0dB. In return, the signals coming back into the console from the digital tape recorder were often 12dB or more above the console’s NOL of 0dBVU, pushing channels and processors to the point that even a small EQ boost could result in clipping, and compressor/limiters were slamming hard even at their highest thresholds. Level chaos reigned – especially when inserting devices between the mixing console and multitrack recorder. Although this problem was quickly resolved in professional analogue studios by in-house technicians who could explain the new digital system’s equivalent to 0dBVU and how to interpret the differences between Peak metering and VU metering, it recurred in the early days of the project studio when recording musicians were connecting digital multitrack recorders such as Alesis’ ADAT (+4dBu = -15dBFS) to analogue consoles such as Mackie’s 8 Bus (+4dBu = 0dB = NOL) and did not have access to studio technicians to advise them on optimum recording levels.

To further add to the confusion, many of the early affordable digital recorders, editors and DAWs were 16-bit systems with low quality converters, fixed-point DSP processing and no dithering – three factors that ultimately gave them poor performance with low signal levels, especially when many channels were being processed and combined together. When used for ‘in the box’ multitrack applications the resulting sound from those early 16-bit systems was often described as ‘gritty’, a word that became perfectly apt when listening to long fade-outs or pieces that contained lots of edits and crossfades happening simultaneously (e.g. a pre-mix edit to remove a verse or chorus across all tracks of a multitrack session file). In multitrack music situations those early 16-bit systems often did deliver a better sounding end result (i.e. less ‘gritty’) when signal levels were kept high, giving credence to the notion that signal levels needed to be kept as close to 0dBFS as possible. Unfortunately, this ‘close as possible to 0dBFS’ practice still lingers despite moving to 24-bit systems with better converters, 64-bit floating point processing and advanced noise-shaped dithering – all of which relegate the grittiness of the early 16-bit systems to a brief moment in audio antiquity.

Gritty-Sweet 16

Concerns over 16-bit word sizes and processing was often shrugged off with the belief that there was no point in going beyond 16-bits because that’s the best that CD could offer – a mathematically ill-informed justification that flew in the face of one of the audio world’s longest held truths: that the capture and production equipment should always have better specifications than the release medium because every step in the production process reduces the quality – particularly in terms of noise. In the analogue world, the accumulated noise of the recording, production and mastering processes (room noise, thermal noise, tape hiss, surface noise of lacquer and stamper) didn’t matter as long as it remained sufficiently lower than the noise of the release mediums, i.e. the surface noise of pressed vinyl or the hiss of cassette tape. The same holds true in the digital world except that the noise of digital systems (thermal noise from analogue input and output circuits, quantisation noise from conversion and processing, dither noise added to de-correlate and hide quantisation noise) is many decibels lower to start with so it’s rarely a problem, even after considerable processing.

To put that into context, some of the earliest studios to adopt digital multitrack recorders quickly discovered that the background noise of their recording spaces and the noise from their consoles (which was all previously buried in tape hiss) was now audible in their recordings and could be heard accumulating with every new track. This was an interesting problem – removing the noise of analogue tape revealed what it was hiding.

Similarly, when using the early fully digital multitrack systems that used 16-bit technology, the accumulated quantisation error noise and its associated ‘grittiness’ became apparent in the absence of any analogue noise (e.g. thermal noise from the analogue mixing console) to hide and/or de-correlate it through inadvertent dithering – which explains why the ‘grittiness’ wasn’t a problem in the early hybrid studios that used analogue mixing consoles with 16-bit digital multitrack recorders. [This is also one of the catalysts behind the ‘summing mixer’ phenomenon, but that’s another story…]

What’s all of this got to do with choosing microphones and setting gain? It highlights the history behind some long-held misunderstandings about signal levels in digital audio systems, and getting signal levels right in digital audio systems is important when choosing microphones and setting gain – as we’ll see shortly.

RP-155

In the early 1990s the Society of Motion Picture and Television Engineers (SMPTE) put forth the RP-155 Standard that recommends an Alignment Level of -20dBFS. According to RP-155, if a 1kHz sine wave with a level of +4dBu enters the digital device’s analogue line input its metering should show -20dBFS, and if that same 1kHz sine wave at -20dBFS leaves the digital device’s analogue line output it should measure +4dBu. RP-155 gives the digital system 20dB of Headroom, which is enough for most music and dialogue applications.

How do the analogue specifications shown earlier fit into a digital metering system that’s aligned to RP-155? We already know the digital system’s Maximum Level (0dBFS) and its Alignment Level (-20dBFS, equivalent to the analogue world’s NOL), which means we can calculate its Headroom (20dB). To calculate a digital system’s S/N Ratio we need to know its Dynamic Range, which we can calculate if we know its word size…

The most common form of digital audio, as used in Compact Disc and wav files, is known as ‘Linear PCM’ (also ‘LPCM’ or simply ‘PCM’). Calculating the Dynamic Range for a Linear PCM system is simple: it is 6.0206dB per bit, although this is commonly shortened to a rule-of-thumb value of 6dB per bit. We’ll use 6dB per bit for the purposes of this exercise. A 24-bit wav file offers a Dynamic Range of 24 x 6 = 144dB, easily exceeding the best that practical analogue circuits can offer. If there is 144dB of Dynamic Range and the maximum level is 0dBFS, the minimum level will be -144dBFS. Allowing a few dB due to quantisation error noise and dither provides a Noise Floor that is still somewhere below -140dBFS.

The illustration below shows how the analogue specifications mentioned earlier fit into a 24-bit digital system and a 16-bit digital system, both aligned to RP-155 so that -20dBFS = +4dBu.

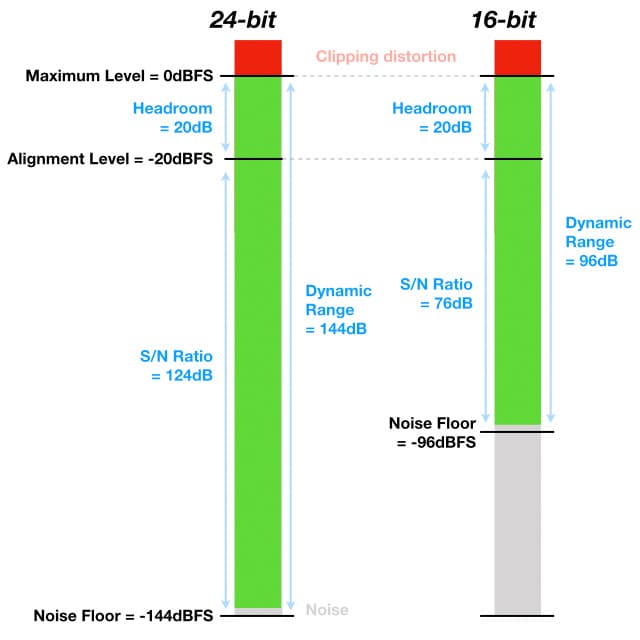
Knowing this information allows us to optimise systems that combine analogue and digital equipment. For example, using the RP-155 recommended Alignment Level of -20dBFS for a digital recorder makes sense if the microphone preamplifier driving it also has 20dB of Headroom – both devices have the same Maximum Level, both will go into clipping at the same time and neither is wasting any of its Headroom capability.

If the microphone preamplifier was a costlier device with 24dB of Headroom then it would make sense to set the digital recorder’s Alignment Level to -24dBFS, otherwise we’re wasting the Headroom capabilities of the microphone preamplifier because the digital recorder will go into clipping before the preamplifier.