
Can You Tell The Decibel?
Coach Covill gets back to basics with a decibel primer, drilling down to the types you should keep your ear out for.
Tutorial: Hugh Covill
The decibel is the common language of audio folk but many remain unsure how to speak this language fluently. There are a plethora of decibel dialects you’ll come across on your audio journey. Here’s just a few off the top of my head: dBm, dBW, dBV, dBmV, dBuV, dBu, dBuA, dBHz, dBSPL, dBA, dBTP, dBSWL, dBSIL… The list goes on and on. In this primer I’ll break decibels down to their nuts and bolts, provide some ‘rules of thumb’ for their usage, argue which flavours are the most essential, and for those who are maths averse, all without citing a single logarithmic equation. Hopefully we’ll traverse the yellow brick road of volts, watts and sound pressure levels to emerge adept and fluent decibel linguists.
WHY THE DECIBEL?
The decibel came out of Bell Laboratories in the 1920s, hence the Deci-‘bel’. The ’20s saw an exponential adoption of telephone use and engineers needed a methodology and scale to quantify signal loss in telephone lines. At that time, the decibel measured the change in power over a mile of standard cable with defined properties. By 1940, the VU meter (using a decibel scale) was adopted across the telephony industry and beyond to broadcasting and recording — the decibel had arrived.
WHAT IS A DECIBEL?
A dB is a logarithmic unit. It describes the ratio (change) between two values. In audio these values are usually power or voltage. Now I promised there would be no maths so I won’t elaborate further on the empirical definition. The key things to understand are:
- A dB is a dimensionless unit in the same way a percentage is. Percentages are used to express how large or small one quantity is relative to another quantity. Decibels describe the change from one volume/voltage/power state to another.
- The dB uses a logarithmic scale. Logarithms are just a way of describing very large numbers as much smaller numbers. A logarithmic scale is a good fit with the way we humans perceive sound.
Here’s a quick example: The range of human hearing (change in sound pressure level) is measured in micro-pascals (μP). The threshold of hearing is 20μP, the loudest rock band might be >20 million μP. You can see the range is huge, but described as a decibel it registers as a change of 120dB. Now, the complete range of human hearing is more like two billion μP!
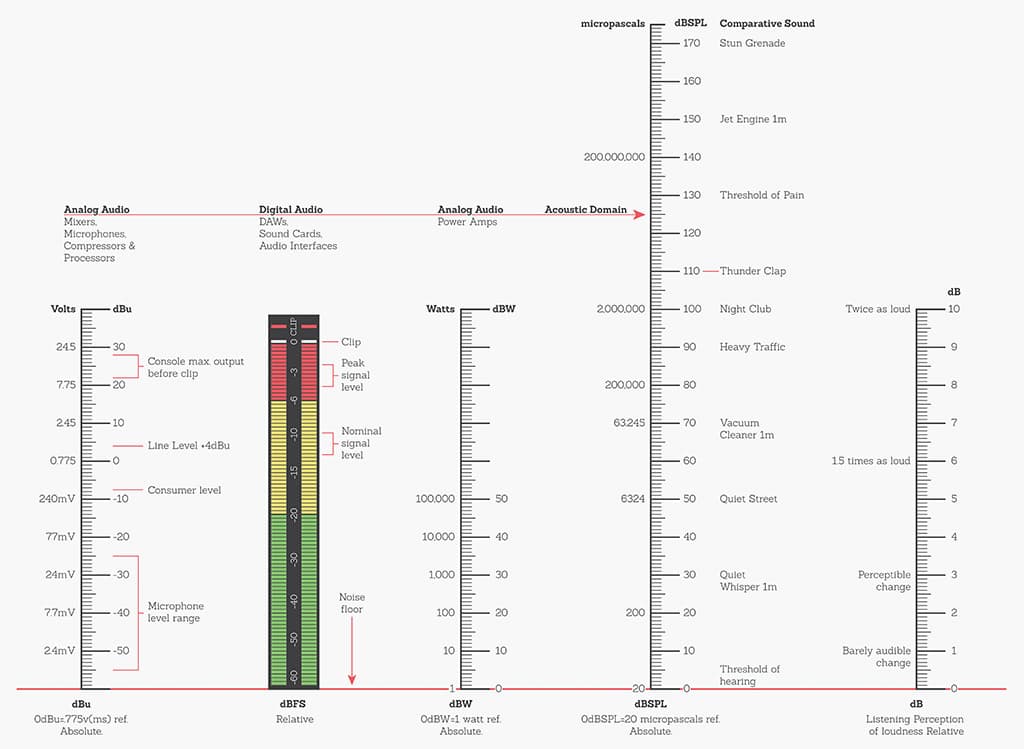
ABSOLUTE & RELATIVE DECIBELS
As a general rule, adding a suffix to a decibel makes the unit absolute. Absolute decibels represent comparative change from a known reference. For example 0dBu is defined as 0.775 volts RMS, 0dBV is defined as one volt RMS, 0dbW is defined as one watt, 0dBSPL is defined as 20 micro-pascals. So, for instance, 22dBu is a change in voltage of 9.75V from the reference level of .775V. You’ll see absolute decibels used in technical specifications for mixing consoles, microphones, compressors, etc.
Relative decibels, on the other hand, measure the proportional change between two values. For example, the proportional change from 5V to 8V is 4dB.
Now I promised not to cite maths so you’ll have to take my word for the above solutions. The important thing to grasp is the difference between absolute and relative. There are a huge number of suffixes in the audio industry and beyond audio the decibel is used in industries as diverse as telecommunications, satellite and antennae design, RF design, radar and microwave technology to name a few. Each has its own set of useful reference suffixes.
So which are pertinent to the modern audio practitioner? It’s my view that there are four key decibel descriptors that are important to understand:
- dBu (Un-terminated) because it’s the standard quantifier for pro audio: +4dBu=0VU
- dBV (to a lesser degree) because it’s still used in many pro audio specs: as a ‘rule of thumb’ dBV = dBu + 2.2
- dBFS (Full Scale) because it’s the metering system almost everyone who is recording digitally will be utilising.
- dBW (Watts) because it’s the standard for pro audio amplifier power description.
- dBSPL (Sound Pressure Level) because it’s the accepted standard descriptor for loudness.
A quick caveat regarding dBFS: Full scale is, in fact, a relative measure. Think about it. There’s no reference quantifier because full scale refers to 0dB being the point at which your audio will go into clip… but that point is dependent upon your bit depth. Bit depth has no relationship to audio resolution — it defines the dynamic range of your digital audio. At 16 bits, your dynamic range is ostensibly 96dB; at 24 bits, it’s 144dB. It’s a little more complex than this, but bottom line, the point at which you ‘run out of bits’ is variable.
Much has been skated across here. If you’re searching for a more comprehensive overview of decibels that includes the logarithmic equations, relationship to gain structure, dynamic range and headroom I wrote a much more comprehensive gain setting tutorial in Issue 47, which you can dig up on www.audiotechnology.com.au by searching ‘Gain Structure’.














Quote : ” There’s no reference quantifier because full scale refers to 0dB being the point at which your audio will go into clip… but that point is dependent upon your bit depth.Bit depth has no relationship to audio resolution — it defines the dynamic range of your digital audio. At 16 bits, your dynamic range is ostensibly 96dB; at 24 bits, it’s 144dB”
I would like to add that bit depth is more related to your AD/DA design specs. Up to date I haven’t heard of any manufacturer that overcame the barrier of 127-132 dB dynamic range in their AD/DA products and that range refers to the converter itself usually. Placing it on a circuit board additional noise is introduced depending on the design . So (correct me if I am wrong) there is no actual 24 bit converter due to various (call me noise) limitations in circuitry design. But that doesn’t necessarily mean that technology will stop evolving…. Sorry for any grammar mistakes in the text, English is not my native language.